📌
'''
OLS : 선형회귀분석을 위한 모델
독립변수와 종속변수의 영향력을 수치로 표시
'''
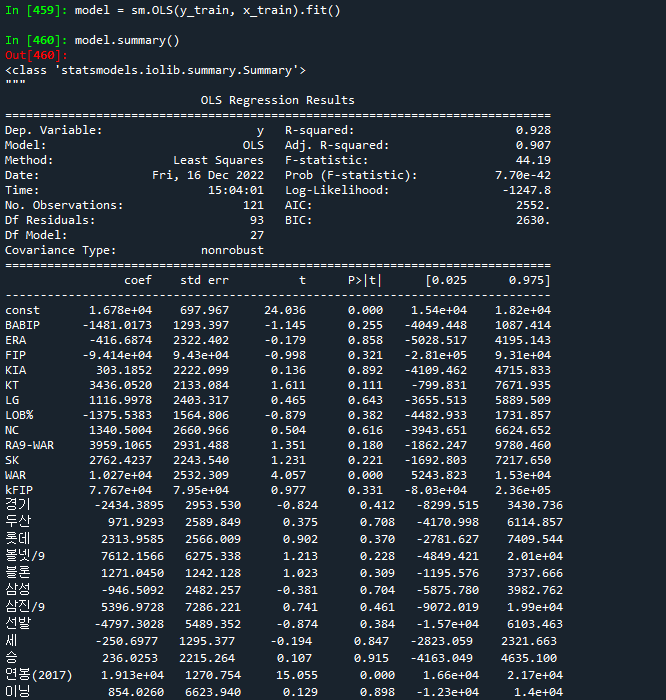
model = sm.OLS(y_train, x_train).fit()
model.summary()
'''
R-squared : 결정계수. 0~1사이의 값.
1에 가까울 수록 수치가 좋음.
독립변수의 개수가 많아지면 값이 커진다.
Adj. R-squared : 수정결정계수.
표본의 크기와 독립변수의 개수 고려하여 수정
=> 독랍변수의 변동량에 따라서 종속변수의 변동량
P>|t| : p-value 값.
0.05미만인 경우 회귀분석에서 유의미한 피처(컬럼)들이다.
WAR , 연봉(2017), 한화 3개의 피처들의 유의미한 피처.
coef : 회귀계수. 독립변수별로 종속변수에 미치는 영향값을 수치로 계산.
회귀계수에 따라서 종속변수가 어떻게 움직이는지 알 수 있다.
'''
# 그래프 출력하기
import matplotlib.pyplot as plt
plt.rcParams['figure.figsize'] = [20,16]
plt.rc('font', family="Malgun Gothic")
plt.rcParams['axes.unicode_minus']=False
coefs = model.params.tolist() # 회귀계수 목록
coefs
coefs_series = pd.Series(coefs)
x_labels = model.params.index.tolist()
x_labels # 컬럼명
ax = coefs_series.plot(kind='bar')
ax.set_title('feature_coef_graph')
ax.set_xlabel('x_features')
ax.set_ylabel('coef')
ax.set_xticklabels(x_labels)

#
from statsmodels.stats.outliers_influence \\
import variance_inflation_factor
vif = pd.DataFrame()
vif["VIF Factor"] = [variance_inflation_factor(X.values, i)\\
for i in range(X.shape[1])]
vif["features"] = X.columns
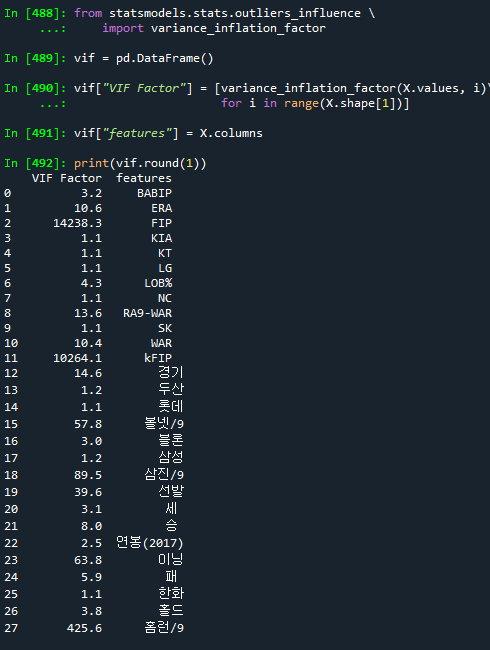
print(vif.round(1))
'''
VIF(variance_inflation_factor) : 분산팽창요인.
독립변수들은 서로 독립적이여야함. 독립변수간의 연관성은 없는게 좋다.
다중 공선성 : 독립변수들 사이에 연관성으로 가중치 발생.
예제에서는 FIP, kFIP 변수는 한개만 선택하는 것이 좋다.
'''
from statsmodels.stats.outliers_influence \\
import variance_inflation_factor
vif = pd.DataFrame() # 데이터 프레임
# X.values : 현재 데이터들
# X.shape[1] : 컬럼의 개수. 28개
vif["VIF Factor"] = [variance_inflation_factor(X.values, i)\\
for i in range(X.shape[1])]
vif["features"] = X.columns
print(vif.round(1)) # 소숫점 한자리에서 반올림 출력

# 회귀분석
from sklearn import linear_model
from sklearn import preprocessing
lr = linear_model.LinearRegression
# 독립변수 선책
X = picher_df[["FIP","WAR","볼넷/9","삼진/9","연봉(2017)"]]
Y
# 훈련데이터(0.8), 테스트데이터(0.2) 분리
x_train, x_test, y_train, y_test =\\
train_test_split(X,Y,test_size=0.2,random_state=19)
lr = lr.fit(x_train, y_train) # 학습
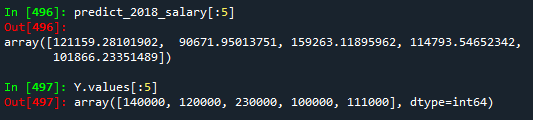
predict_2018_salary = lr.predict(X) # 예측
predict_2018_salary[:5]
Y.values[:5]
# 2017 연봉과 2018연봉이 다른 선수들만 10명을
# 작년 연봉, 예측연봉, 실제연봉 그래프 출력
# 2018년 연봉이 가장 많은 선수 10명만 그래프로 작성
# 예측연봉
picher_df["예측연봉"] = pd.Series(predict_2018_salary)
picher_df["예측연봉"]
# 2017년도 연봉
picher_df["연봉(2017)"]
picher["연봉(2017)"]
# picher_df["연봉(2017)"] 컬럼 제거
del picher_df["연봉(2017)"]
# picher["연봉(2017)"] 컬럼을 picher_df["연봉(2017)"]에 저장하기
picher_df["연봉(2017)"] = picher["연봉(2017)"]
picher_df["연봉(2017)"]
# picher_df["y"] 컬럼에 picher["y"] 저장하기
picher_df["y"] = picher["y"]
picher_df["y"]
# 선수명 저장
picher_df["선수명"] = picher["선수명"]
picher_df.info()

# 2018 연봉의 내림차순으로 정렬하기
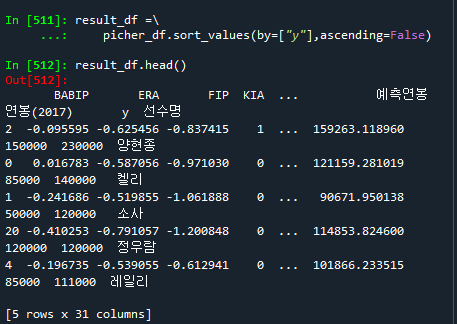
result_df =\\
picher_df.sort_values(by=["y"],ascending=False)
result_df.head()
# "선수명","연봉(2017)","y","예측연봉" 만 가지고 오기.
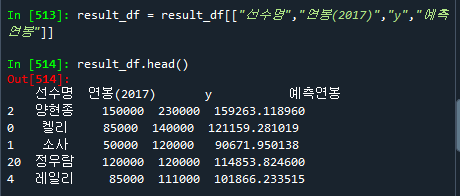
result_df = result_df[["선수명","연봉(2017)","y","예측연봉"]]
result_df.head()
# y 컬럼을 실제 연봉 컬럼으로 이름 변경
result_df = result_df.rename(columns={"y": "실제연봉"})
result_df

# 작년연봉과 실제 연봉이 다른 선수들 10명만 출력하기
result_df = result_df[result_df["연봉(2017)"] != result_df["실제연봉"]][:10]
result_df
# 그래프 작성
result_df.plot(kind="bar",x="선수명",y=["연봉(2017)","실제연봉","예측연봉"])

📌
###############################
# 회귀분석 - 결정계수
# 1에 가까울 수록 성능이 좋다
lr.score(x_train, y_train) # 0.9276949405576705
lr.score(x_test, y_test) # 0.886017164497782
######### rmse 값
# mse(mean squared error) : 평균제곱오차. 작은값일수록 성능이 좋다.
# rmse : mse의 제곱근.
from math import sqrt # 제곱근 함수
from sklearn.metrics import mean_squared_error # mse함수
y_pred = lr.predict(x_train) # 훈련데이터 예측
sqrt(mean_squared_error(y_train, y_pred)) # 7282.718684746373
y_pred2 = lr.predict(x_test) # 테스트데이터 예측
sqrt(mean_squared_error(y_test, y_pred2)) # 14310.69643688912
# 과대적함(과적함) : 훈련데이터의 검증값 > 테스트데이터의 검증값
# 훈련데이터의 검증값 = 테스트데이터의 검증값
'수업(국비지원) > Python' 카테고리의 다른 글
| [Python] 반 정형 데이터 - 한글 분석 (0) | 2023.04.27 |
|---|---|
| [Python] 지도학습 예제 - titanic (0) | 2023.04.27 |
| [Python] 머신러닝 - 지도학습(분류) 3. Decision Tree(의사결정나무) (0) | 2023.04.26 |
| [Python] 머신러닝 - 지도학습(분류) 2. SVM (0) | 2023.04.26 |
| [Python] 머신러닝 - 지도학습(분류) 1. KNN (0) | 2023.04.26 |



